株価予想は数学的に不可能

2023年に入り、エコミストたちが我こそはと次々株価予想を打ち出しています。

エコノミストたちは、株価の精度を競っているわけではなく、どうしてそうなるかのストーリーでバトルしているだけなのですが、本記事ではこれを真正面から受け止め、株価予想が数学的に不可能であることを、数学を使わず感覚的に解説します。

数式は一切出てこないのでご安心を。。。

※詳しい人のために・・・本記事では、共和分の話は、ややこしいし実務上のメリットもあまりないのでしません。念のため。

株価は単位根の性質を持つ
単位根は見せかけの回帰を引き起こす
単位根はどれほど悪影響か
単位根は実務のプロにも認知されていない
変化率は分析可能
まとめ

株価は単位根の性質を持つ

2021年2月に日経平均株価が3万円を超え、日本の市場関係者は30年ぶりの快挙で大いに沸き立ちました。
結局、日経平均は3万円台を維持できませんでしたが、それから日経平均3万円論を目にしない日はありませんでした。

未だに我々は1989年の史上最高値に縛られているわけですが、ここに、数多の学術研究を白紙に帰した統計分析における最悪の罠”単位根”が潜んでいます。

単位根は、簡単に言えば、”過去の影響がいつまでたっても消えない”という性質です。

日経平均株価で言えば、史上最高値を更新できるかどうかのところに値が近づくと、どうしても30年前が頭にチラついてしまうような、そんな性質を単位根と呼びます。

単位根は見せかけの回帰を引き起こす

過去の影響がいつまでもチラつくのがどうして悪いことなのでしょうか？

まずは下の図をご覧ください。

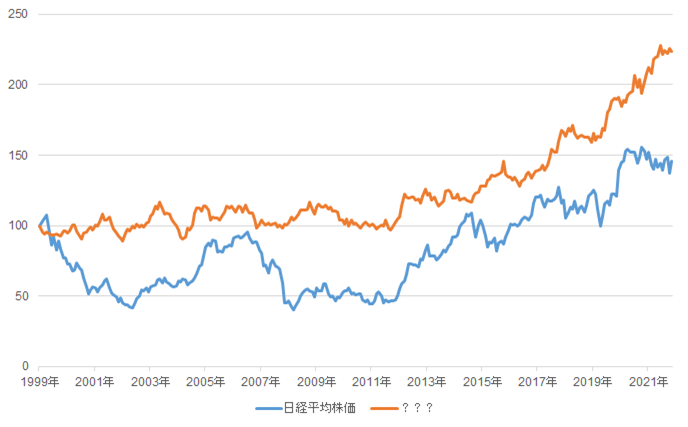
1999年12月31日を100として、青い線は日経平均株価を、オレンジ色の線は別の指標の推移を示したものです。
日経平均株価のデータ出所：https://indexes.nikkei.co.jp/nkave/archives/data

見た感じ、なんか似たような動きをしていますよね。
決定係数（相関のようなもの）は0.74と極めて高いので、オレンジの指標が何なのか分かれば、青い線が上昇するタイミングをおおむね捉えることができます。

実はこのオレンジの線は、単位根の性質を持った乱数をテキトーに発生させて作った線です。

つまり何が言いたいかというと、

単位根の性質を持ったデータ同士を分析にかけると、本来全く関係ないのに、まるで関係があるような分析結果が出てしまうのです。

このクライヴ・グレンジャーとポール・ニューボールドが1974年にシミュレーションで発見した現象は見せかけの回帰と呼ばれ、1986年にピーター・フィリップスによって数学的に証明されました。
グレンジャーはこれに関連する一連の研究の功績により、2003年にノーベル経済学賞を受賞しています。

何が起きているのかを感覚的に説明すると、

2つのデータには過去の情報が消えずに残り続けているので、ある時期の情報が別の時期の情報と関連を持ってしまう

というようなイメージのことが起こっています。
雑に例えると、データAが2005年10月には上昇していたという情報と、データBが2020年4月に上昇していた、という情報が相関として出てしまうのです。

単位根はどれほど悪影響か

この単位根を知らないことが、どれほどの事態を引き起こすかを象徴しているのが、デイビッド・レインウェイバーが1995年発表（2007年に論文化）した“Stupid Data Miner Tricks: Overfitting the S&P 500”に記された話で、彼は、

バングラデシュのバターの生産量がS&P 500の動向を75％の精度（決定係数が0.75）で予測できること、そして、そこに米国のチーズの生産量を含めると精度が95％まで上昇することを述べました。

当然この2つにしっかりとした関連性は無く、この手の分析が誤りであることを警鐘するために書かれたものです。
しかし、レインウェイバーによれば、発表後には、S&P 500の動向を知りたい人間からバターの生産量に関する問い合わせが後を絶たないらしいです。

このふざけた話は世界中の投資家に鼻で笑われて終わったのですが、これが、「金融政策は２年ほどのタイムラグを経て本格的に効果が発揮される」という話だったら見抜けたでしょうか？

単位根の危険なところは、素人には判断が困難であることです。
大学院でちゃんとしたトレーニングを受けた人であれば「このグラフは単位根があるかもしれないな」という推察は可能ですが、本当に単位根があるかどうかは専用の分析を行ってみないと判断は困難です。

グラフを見て「この2つのデータは関連がありそうだ」と思った時には、この落とし穴にハマっている可能性があります。

単位根は実務のプロにも認知されていない

単位根は、ここ20年ほどの間に大学院で専門的なトレーニングを受けていれば必ず知っている（むしろ知らなければかなりやばい）事項なのですが、金融業界には、視覚的にグラフの類似性を主張する事例が後を絶ちません。

言論プラットフォームのアゴラにて、慶応大学名誉教授の池尾和人先生が、高橋洋一氏の初歩的な誤りを指摘しています。
アゴラの記事はこちら：https://agora-web.jp/archives/1583767.html

初っ端からキツイ言葉で次のように書かれています：

高橋洋一氏が、「金融政策には効果ラグがあり、政策を行ってから２年程度のラグで本格的な効果が発揮できる」と主張する根拠は、たぶんこのディスカッション・ペーパー（PDF）のp.13の図９に示されたような分析だと思われる。しかし、少なくともこの分析は、時系列データの取り扱いに関する基本的な理解を欠いたものだと言わざるをえない（グローバルセキュリティ研究所にも、もう少ししっかりしてほしい）。
見せかけの回帰（かなり技術的）

安倍政権の経済政策ブレーンを務める人間ですら、油断すると見落としてしまうのが単位根の恐怖なのです。

単位根で失敗しないためには、素人が不用意にデータ分析しようとするのは止めた方が良いでしょう。
なぜなら、金融関連のデータはだいたい単位根の性質を持っていると言われています。

特に、「○○はランダムウォーク」ということが言われるようなデータに触るのは避けるのが良いでしょう。
ランダムウォークは単位根の性質を持つデータの一種ですので、例えば、株価はランダムウォークと言われますが、株価はまさに単位根の性質を持っていることが多いです。